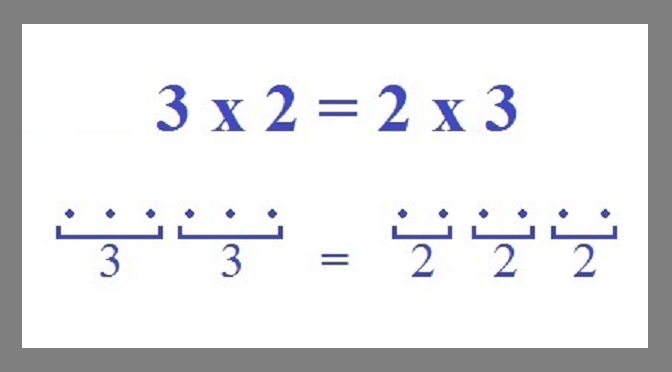Hemiola (Part I)

The healthy human mind loves being active, recognizing patterns and especially solving puzzles.  That applies even to math puzzles.  Perhaps because of the way mathematics is taught in our society, a lot of people have to come to believe that they dislike or fear the subject.  Yet one of the reasons why they enjoy music is the little math puzzles that are often presented to them — and then solved — in music.

The commutative law of multiplication tells us that 3 x 2 gives the same result as 2 x 3.  So if you have 2 groups of 3 units each, the total number of units is the same as it would be for 3 groups of 2 units.

A rhythmic device in music known as hemiola takes advantage of this mathematical fact.  (The word “hemiola” comes from the roots “hemi” (half) and “holos” (whole).  A half and a whole add up to the number 1.5, or equivalently the ratio 3:2.)

The device is used within a piece of music where pulses regularly appear in groups of 3.  But within the hemiola, 3 groups of 2 pulses are substituted for the expected 2 groups of 3 pulses, disrupting the surrounding rhythmic flow.  When the hemiola begins, the listener is presented with a sudden disturbance in the rhythmic order, which may cause momentary confusion and puzzlement.  But the puzzle is solved as the hemiola completes after 6 pulses, thus ending at a normal boundary for the meter of the piece.  The underlying rhythmic order remains intact, through the musical realization of the equation 3 x 2 = 2 x 3.

The pulses can be whole beats, or they can be fractions of a beat.  This example in the pic is from my Romance for Oboe and Piano, showing the oboe part by itself.  The piece is in 12/8 meter, which means that there are 4 beats to each measure and each beat naturally subdivides into 3 pulses, each pulse having a value equivalent to an eighth note.

In the first two full measures of the excerpt, the rhythm follows the normal pattern as implied by the 6/8 meter, and the beats are naturally subdivided by the ear into 3 pulses each.  In the third measure, however, the pulses suddenly seem to arrange themselves into groups of 2, causing a momentary sense of chaos.  The sensitive listener feels a great disturbance in the force — but it is only momentary.  The first three groups precisely occupy two beats of the measure, and the last three groups occupy the other two beats.  Thanks to the magic of the commutative law, our sense of order is restored.  This passage can be heard and followed along with the score in this video, beginning around 0:30 into the video.

The next example is from the Andante grazioso movement of my Sonata for Oboe and Piano, which is in 6/8 meter.

In 6/8, the measure normally consists of 2 beats, which naturally subdivide into 3 eighth-note pulses each.  Here the oboe part is consistent with that regular rhythmic order.  The right-hand chords in the piano part, however, are presented in hemiola fashion, with each chord having a duration of just 2 eighth-note pulses.  Within each measure, there is a sense of momentary chaos, but the two instruments arrive at the following downbeat together, because of the commutative law.  The passage starts around 3:10 in the video.

 

Both of these examples have been at relatively slow tempos.  A subsequent Part II post will present further hemiola examples that are more up-tempo and use other instruments.  UPDATE:  Part II is here.