Fearful Symmetry

“What immortal hand or eye
Could frame thy fearful symmetry?”

— William Blake

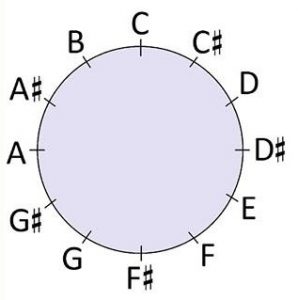
Based on the principle of octave equivalence, we can think of “C” as representing all the various C pitches on the keyboard, plus all the theoretical C pitches beyond the ends of the keyboard.  “C-sharp” represents all the possible C-sharps and D-flats, and so on.  There are then twelve different pitch classes, which can be conveniently represented on a clock face.  Music theorists often represent these pitch classes by integers 0 to 11, but we can use the more familiar letter names here.  So we put C at 12:00, C-sharp at 1:00, and so on.

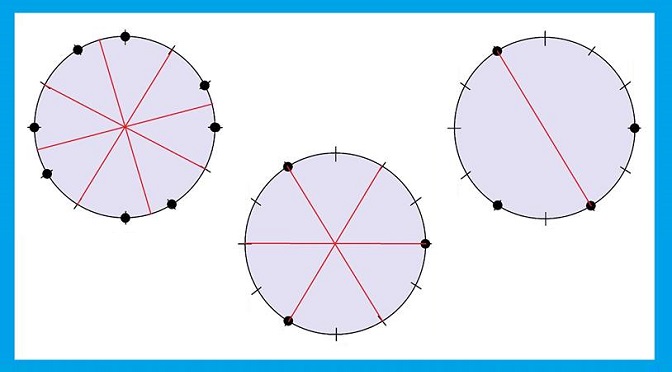
We can then represent all the possible pitch class sets — or “sets” for short — by dots selecting particular points on the clock face.

Clockface notation is especially useful for demonstrating the symmetrical structure of certain sets.  As it turns out, composers of the late Romantic period show a preference for symmetrical sets.

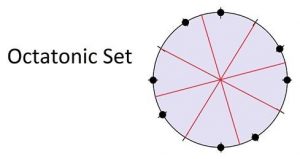
A good example is the octatonic set, which was used frequently in this period and which I introduced in an earlier post to this blog.  In fact, the scale formed by its pitches is sometimes called the Korsakovian scale, because of its association with Nikolai Rimsky-Korsakov and other composers around him.  The illustration below shows one of the three possible octatonic sets.  I have shown in red the four axes of symmetry about which this octatonic set is symmetrical.

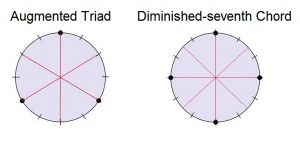
If you draw the diagrams for the most common chords of classical harmony on a sheet of paper, you will find that most of them do not exhibit symmetry.  The major and minor triads and the dominant-seventh chord (i. e., Mm7) are all asymmetrical.  On the other hand, the augmented triad and diminished-seventh chord and augmented triad are symmetrical, and both of these received increased emphasis during the late Romantic period.

In a post to this blog in April, I discussed the elided 2, a frequent feature of Rachmaninoff’s music, which I discovered while working on my PhD dissertation on that composer’s harmonies.  Instead of the normal descent from scale degree 3 through 2 to scale degree 1 over a progression from tonic to dominant to tonic, scale degree 2 is elided, resulting in an unusual and sensuous unresolved dissonant sonority over the dominant.  The sonorities created in this manner are very idiomatic to Rachmaninoff, especially when they occur within the minor mode.  At the end of that blog post on the elided 2, I raised the curious question:  Why does Rachmaninoff have a special predilection to the use of this device in minor keys?  The notion of symmetry gives us a possible answer.

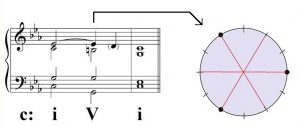
When scale degree 2 is elided over i-V-i harmony, the resulting sonority is an augmented triad (also describable as III+6), which as we have observed is symmetrical:

The same elision over i-V7-i harmony results in a four-note sonority that is not so conveniently described, but which is also symmetrical:

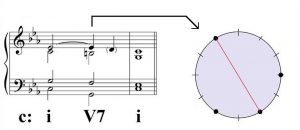
Rachmaninoff most often uses this device in minor keys.  The elided 2 in major mode does not produce symmetric sonorities, as can be determined by changing the key signature to C major in the examples above.  Eliding scale degree 2 in a I-V-I progression in C major gives us a very weak I-iii-I progression, where the minor iii triad is asymmetrical.  The elided 2 in I-V7-I creates a much stronger progression, but the resulting sonority (G-B-E-F) is asymmetrical.

Some historians have attributed Rachmaninoff’s preference for minor keys to Russian fatalism or melancholy.  But perhaps the composer favored the minor mode for a more technical reason:  It is abundant in symmetrical sonorities.